La tablilla Plimpton 322 es la responsable de hacer quedar a Pitágoras como un aprovechado de lo que ya sabían los babilonios 1000 años antes que él. Así, lo demuestran las investigaciones y resultados de la tablilla de la antigua Babilonia estudiada por Edgar Banks. Pitágoras nos engañó y su teorema es más babilónico. ¿Por qué sigue siendo de Pitágoras?

Diseño de Imagen: Ludwin L. Venera// Exclusividad Comunicar Noticias
Las matemáticas siempre han vivido misterios a raíz del teorema que hoy lleva el nombre de Pitágoras. Uno de los más antiguos teoremas matemáticos está por cambiar de nombre. El hecho inició desde el momento que el investigador Edgar Banks analizó unas antiguas tablillas babilónicas. Al parecer el hecho que hayan sido escrita mil años antes que la existencia de Pitágoras, esta demostrando que no fue en Grecia donde realmente se desarrollo este teorema. Sino en Babilonia. Los resultado nos dice que ¡Pitágoras nos engañó! El teorema no es de el. Por lo tanto, debería ser atribuido a los babilonios.
El nombre de Edgar Banks quien fue arquitecto y novelista norteamericano entre (1866-1945), sirvió de inspiración para el famoso personaje de Indiana Jones; realizó investigaciones importante entre ellas interpretar la tablilla Plimpton 322. Con ella afirmó que en Babilonia se usó el teorema de Pitágoras. ¿Cómo es posible si Pitágoras aún no existía? Entonces, el misterio tiene una sola respuesta. Pitágoras nos ha venido engañando.
Te puede interesar: Galileo un heredero de la astronomía copernicana (I)
Plimpton 322, todo un misterio

Cortesía diario Ancient Origins
La tablilla fue descubierta en la ciudad de Larsa, al sur de Irak, a comienzos del siglo veinte y actualmente permanece en la Biblioteca de Libros Raros y Manuscritos de la Universidad de Columbia (Nueva York). Su nombre hace referencia al editor neoyorkino George Arthur Plimpton que la compró en 1922.
El contenido del la tablilla, contenía una tabla trigonométrica. Cuyos cálculos son necesarios usando el teorema de Pitágoras. Entre otros conceptos dados por los griegos. Sin embargo, todo indica que no fue Pitágoras quien enunció por primera vez el teorema. Mil años antes los Babilonios ya tenían claro esos cálculos.
Te puede interesar: El misterioso número π desde sus orígenes
Fue en el siglo VI a.c. Cuando Pitágoras de Samos enunció el teorema diciendo lo siguiente:
El cuadrado de la suma de los catetos, es igual a su hipotenusa elevada al cuadrado
De hecho, lo enunció años después de que Hiparco de Nicea «inventara» la trigonometría. Para descifrar el contenido de la tablilla se necesitaron tres idiomas elamita, babilonio y persa antiguo.
Te puede interesar: Hijo de Einstein y padre de los cosmos: Stephen Hawking
Interpretaciones de la tablilla
Es increíble que una tablilla babilónica de hace mas de 3000 años nos enseñe muchas cosas. De hecho, podemos considerar que sus interpretaciones «están a la moda», una tablilla que muestra una breve tabla de resultados trigonométricos para triángulos rectángulos de distintos tamaños. También, se podría afirmar que los cálculos trigonométricos son muchos más avanzados que la trigonometría moderna.
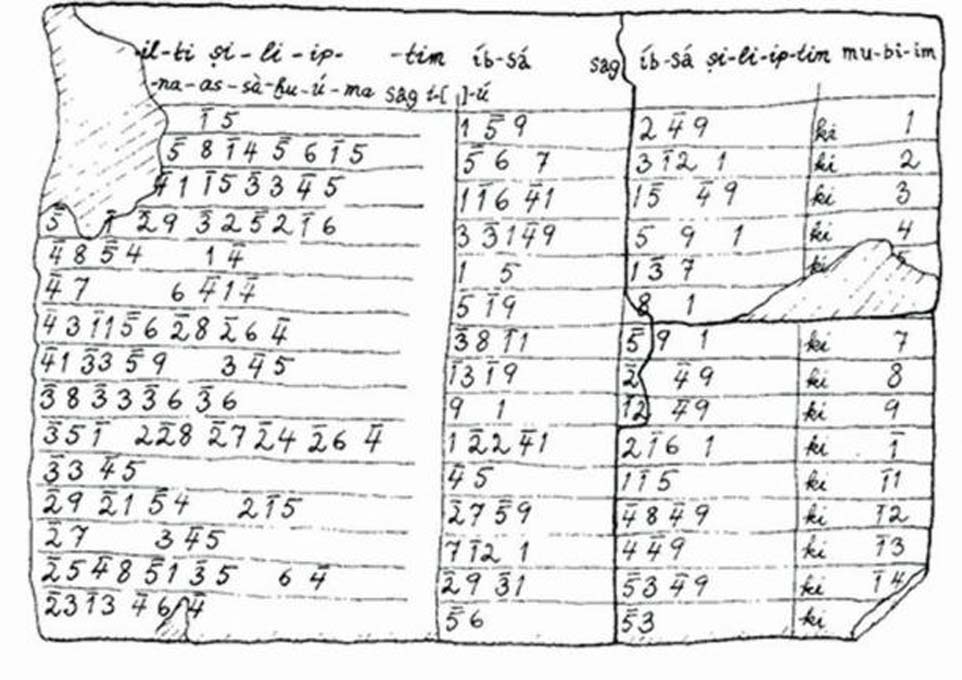
Cortesía diario Ancient Origins
En cada fila esta la muestra de que Pitágoras nos engañó. En cada una de ellas se evidencia razones de series de triángulos rectángulos, que van desde casi un cuadrado hasta en línea recta. Estos resultados, convierten a la Plimpton 322 en una poderosa herramienta que pudo haber sido usada en construcciones de casas, medición de terrenos e inclusive cálculos arquitectónicos para la construcciones de palacios, templos o pirámides escalonadas.
La manera en la que la tablilla dice que los babilonios usaron las matemáticas y la geometría nos dicen más que eso. No es solo la tabla trigonométrica más antigua del mundo, es la más exacta en todo los registros. En la tabla se evidencia que la antigua Babilonia trabajaban con un sistema de base 60, en la actualidad usamos un sistema de base 10. Con ello median los tiempos, lo que significa que trabajaban con fracciones con alto índice de precisión.
Aunque suena como algo poco grandioso, realmente este mecanismo detallado en la Plimpton 322 les permitían a los babilonios hacer divisiones con mucha exactitud. Por ejemplo, una hora divida entre tres, lo daban con el resultado de 20 minutos, lo que es exactamente un tercio de la hora. Esto nos dice que, los babilonios evitaban realizar cálculos inexactos.
El sistema babilónico muestra un potencial enorme, con muchas aplicaciones en topografía, computación y educación. Lo cual nos permite decir que, los babilonios después de mas de 5 mil años nos han enseñado algo nuevo. De hecho algunos matemáticos en el mundo consideran que las matemáticas babilónicas están nuevamente de moda.
Una tablilla que existe desde los años 1830 A.C contra un Pitágoras de Samos, un filosofo y matemáticos que vivió entre los años 570-465 A.C; el descubrimiento de la Plimpton 322 dejó claro que, el teorema no es pitagórico. Realmente Pitágoras nos engañó. Los matemáticos babilónicos utilizaron y colocaron en práctica el famoso teorema geométrico.
Es bien sabido que los griegos le dieron fundamento teórico a las matemáticas. De hecho, sabemos que Euclides de Alejandría en sus 5 tomos, escribió por primera vez la matemática con razonamiento lógico con la creación de postulados, definiciones y teoremas resueltos con la ayuda de la lógica. Esto implica que, fueron los griegos quienes le dieron sentido lógico y científico a las matemáticas. Pero es falso atribuir un teorema que existió mas de 1000 años antes que lo demostrado por los griegos. En efecto, el teorema es más babilónico.
Lecturas recomendadas:
¿Cómo las matemáticas se relacionan con el amor y la pasión?
Goldbach noqueo a Euler con su conjetura sobre números primos
Leonhard Euler: Un matemático con los pies sobre lo «imaginario»
Un amigo de la paz y enemigo de Hitler (I): Albert Einstein
Galileo un heredero de la astronomía copernicana (I)
Gamers Vs Docentes digitales (II): una batalla entre la educación y los vídeo juegos