Las matemáticas suelen tener misterios que aún siguen sin resolver. Su historia ha entregado un sin número de problemas resuelto y los orígenes de esta ciencia abstracta se dio gracias a las necesidades de los hombres. Muchos matemáticos trabajaron durante muchos años sobre lo real. Sin embargo, lo imaginario también es un asunto de las matemáticas. Alrededor de los años 1749, Leonhard Euler se interesó en los números imaginarios, y logró dar con ellos. Euler fue un matemático con los pies sobre lo «imaginario».

Los imaginarios antes de Euler
Los números imaginarios realmente no fueron realmente un descubrimiento de Euler. Matemáticos de siglos antes de lo presentado por el suizo ya habían hablado de estos números. Los primero fueron los matemáticos Niccolo Fontana (alias Tartaglia) y Gerolamo Cardano. Luego, en 1777 Leonhard Euler le dio representación con el símbolo «i», que es exactamente la raíz cuadrada de -1, matemáticamente se escribe √-1.
Para llegar al número i, se tuvo que admitir que las raíces de los números negativos eran simples expresiones reales que representaban una igualdad numérica o solución a un problema. Gardano, por ejemplo, planteó el siguiente problema matemático:
Dividir el número 10 en dos partes, de tal forma que una de las partes, multiplicada por la otra, de 40
La solución al siguiente problema de Gardano fue:

La operación de Gardano es fácil de verificar, en la época el hecho que la verificación permitiera operaciones de suma y multiplicación, la cuales son básicas en el conjunto de los números reales le daba cierta validez. Por lo tanto, el problema estaba resuelto para los años mil quinientos. Fue maravilloso, fue la primera vez en la que se dejó constancia de la representación o solución de un problema matemático con raíces negativas y su manejo algebraico. Sin embargo, para los matemáticos de la época, no tenia sentido dar soluciones de problemas con raíces de números negativos.
Gardano le dio las gracias a Bombelli desde el cielo

Rafael Bombelli (1526-1572), escribió detalles de las raíces de números negativos, en su obra L’Alegebra Opera. Cortesía Formato siete
Rafael Bombelli fue un arquitecto e ingeniero italiano que no dejo el trabajo de Gardano a la deriva, soluciono casos particulares de ecuaciones cubicas o de tercer grado utilizando los métodos de Gardano. Entre la más reconocida fue la ecuación x3=15x+4. Bombelli en su obra detalló su solución y obtuvo para x el valor de 4. Debemos tener en cuenta que en la actualidad la ecuación realmente tiene tres soluciones para la vairable «x». Sin embargo, en la época era difícil considerar los valores negativos. Por lo tanto, Bombelli tampoco.
Te puede interesar: Galileo un heredero de la astronomía copernicana (I)
Rene Descarte si que tuvo imaginación numérica

Cortesía OFrases.com
Rene Descarte dos siglos y medios. Alrededor de 1960, dejó claro el error de Bombelli y Gardano. Las ecuaciones tienen la cantidad de raíces que indique el grado del polinomio. Aunque, alguna de ellas no sean reales; a estos Descarte los denominó, números imaginarios, en la época también fueron llamados números falsos.
El resultado de Descarte causo un impacto en las academias matemáticas del siglo XVIII. Ingenieros, matemáticos de la época cambiarían sus trabajos para incluir el concepto de números imaginarios en los libros.
Te puede interesar: Interpretación geométrica de ecuaciones cuadráticas y cúbicas
Leonhard Euler le puso nombre matemático a lo imaginario
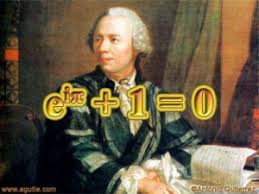
Cortesía Egutie
Euler fue un matemático suizo humilde y de los más grandes escritores de esta ciencia, lo dicen claramente sus 850 obras matemáticas. A pesar de quedar ciego en el año 1771, continuó con sus labores junto a otros asistentes. Gracias a el i=√-1, a esta cantidad la llamó unidad imaginaria y fue fundamental para trabajar su famosa identidad conocida como: la identidad de Euler.
En su obra, Euler explicó la razón de llamar a estos números imaginarios. Esto dijo en su obra Algebra:
Ya que todos los números que es posible concebir son mayores o menores que 0, o son 0 en sí mismo, es evidente que no podemos clasificar la raíz cuadrada de un negativo número entre los números posibles, y por lo tanto debemos decir que es una cantidad imposible. De esta manera esto nos conduce a la idea de números, que por su naturaleza son imposibles; y por eso se les suele llamar cantidades imaginarias, porque existen meramente en la imaginación.
Para no ser condenado o acusado por abusar de su imaginación matemática aclaró en su obra lo siguiente:
A pesar de esto, estos números se presentan ellos mismos a la mente; existen en nuestra imaginación, y todavía tenemos una idea suficiente de ellos; […] nada nos impide hacer uso de estos números imaginarios y emplearlos en el cálculo.
Definitivamente Euler fue un matemático con los pies sobre lo «imaginario». Un matemático que no se le escondió a la naturaleza de los números. Viajo al país de las «mate-maravillas» y le dejo un mensaje claro a Gauss, Hamilton y otros matemáticos que siguieron el trabajo de Euler, lo mejoraron y hoy en día es una teoría más de las matemáticas. Una útil y necesaria.
Definitivamente, Bombelli, Gardano y Descarte, terminaron teniendo la razón. ¿Quién dijo que no podemos usar la imaginación en las matemáticas? La historia te demostró que si.
Documentos de interés: